
投資家がポートフォリオの組み合わせを考える際の格言として、「卵はひとつのカゴに盛るな」というものがあります。理由は、ひとつのカゴに卵を入れてしまうと、そのカゴを落とした時に全ての卵が割れてしまうからです。しかし、複数のカゴに卵をいれておけば1つのカゴを落としても他のカゴにある卵は無事です。
これを株式投資に当てはめると、「ひとつの会社の株を買うのではなく分散投資をしろ」ということになります。この分散投資の裏付けになるのが、現代ポートフォリオ理論という1952年に発表され、のちにノーベル経済学賞を受賞した理論になります。
本記事では、現代ポートフォリオ理論を分かりやすく、極力数式を用いずに解説いたします。
結論
現代ポートフォリオ理論とは?

現代ポートフォリオ理論( Modern portfolio theory, MPT)とは、金融資産への投資比率(ポートフォリオ)を決定する理論です。
1952年にハリー・マーコウィツ(Harry Markowitz)よって発表された理論で、マーケットポートフォリオ(全ての証券を時価総額に比例して保有したポートフォリオ)が一番リスクに対してのリターンが最大化された最適なポートフォリオであるということを述べています。
同理論はのちの金融工学(Financial engineering)の歴史の始まりとなるような大事な理論となっています。
現代ポートフォリオ理論が使われている事例
現代ポートフォリオ理論はインデックス投資の優位性を裏付ける大事な理論であり、こちらの考え方は日本国民の年金を運用する機関であるGPIF(Government Pension Investment Fund)を含めて全世界の機関投資家によって活用されています。
インデックス投資に関しては下記の記事をご覧くださいませ。
前提条件(最適なポートフォリオの定義)
まず、同論文の仮定条件として”投資家は合理的でリスク回避的である”ということが仮定されています。つまり、同じリターンを上げられる資産ならばリスクの小さいものの方が良いという考えが前提となります。
※金融におけるリスクとはボラティリティ(価格変動の度合い)のことで、統計学で言う標準偏差(データの散らばり具合)です。
つまり、”最適な”ポートフォリオの定義はとっているリスクに対してリターンが最大化するようなポートフォリオということになります。
最適なポートフォリオの見つけ方【リスク・リターン平面】
次にHarry Markowitzが最適なポートフォリオを見つけるためにやったこととして、この世にある全てのリスク資産(株式、債券、不動産、コモディティ等)の保有割合を変えながら、その時のリスク(標準偏差)と期待リターンをプロットしました。
例) ・株70%と債権30%で運用した時のリスクとリターンを計算してプロット。その後株71%と債権29%で運用した時も同様にプロット。以下繰り返し。
すると、x軸をリスク(標準偏差),y軸をリターンとして下図のように無数の点がプロットされます。

有効フロンティアとは
その後、先ほどの前提条件に従って、同じリスクならリターンが高いものの方が良いという考えのもと、合理的な点だけ抽出すると下図のように青い曲線の上半分が浮かび上がります。この曲線を有効フロンティア(efficient frontier)と呼びます。
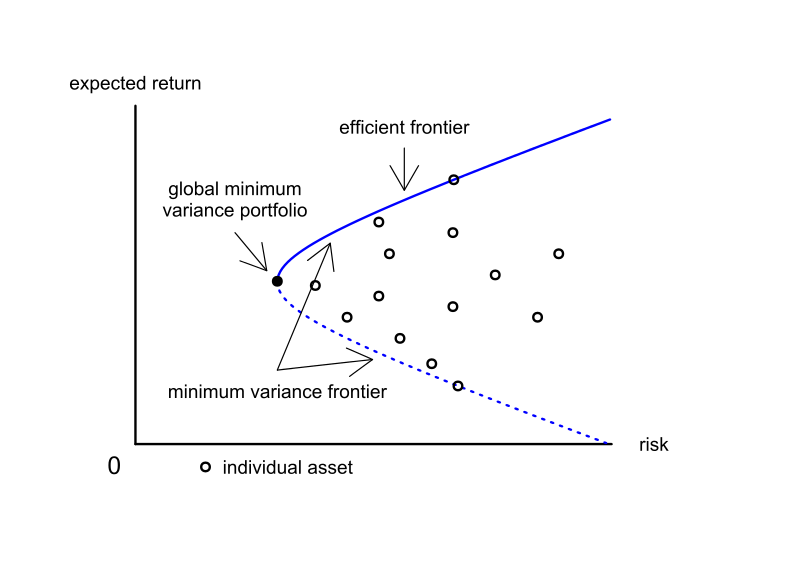
すなわち有効フロンティア上の各点の下にあるような点は全て、非合理的なポートフォリオの配分になっている点と言えます。
接点ポートフォリオが最も効率性の高いポートフォリオ
現時点では、Harry Markowitzが追い求める最適なポートフォリオの配分は、有効フロンティ上にあるということは言えますが、コレだ!!と定められるような1点はまだ断定できていません。
しかし、このリスク資産だけで構成された無数のポートフォリオに、無リスク資産(国債などのノーリスク資産)の保有割合を加えると最適なポートフォリオは一点に決まります。
そうするには、CAPM(資本資産価格モデル,capital asset pricing model)という考え方が必要になってきますが、簡単にご説明するとまず下記のような資本市場線(Capital Market Line)の関数を考えます。

その後、最適なポートフォリオとなる点(リスクに対してのリターンが最大化される点)を特定するために、先ほどの式の傾きに該当する部分(𝜎𝑝の係数)が最大化するように直線の傾きを動かすと、下図のように、有効フロンティア(曲線の上半分)に接する点(接点ポートフォリオ)が最適なポートフォリオの点となります。
接点ポートフォリオ=マーケットポートフォリオ
説明が長くなるため本記事では省きますが、CAPMによると、この接点ポートフォリオこそがマーケットポートフォリオ(全ての証券を時価総額加重平均型に保有したポートフォリオ)ということになります。
参考①) 時価総額加重平均型とは?
Amazonの時価総額がトヨタの時価総額の10倍ならば、Amazon株の保有額もトヨタ株の10倍持つように配分したポートフォリオ
参考②) 接点ポートフォリオ=マーケットポートフォリオになる簡易的な理由
この論文の前提条件として"全ての投資家は合理的である"と述べてます。これを踏まえて、仮に接点ポートフォリオ≠マーケットポートフォリオとすると、全ての投資家はより合理的でおる接点ポートフォリオに近づけるために自分のポートフォリオを接点ポートフォリオに近い配分にします。すると、証券の価格は需要と供給で決まりますので、マーケットポートフォリオは接点ポートフォリオに限りなく近いていって、最終的には同じものになります。
CAPMについて詳しく知りたい方は下記よりご覧になってください。 en.wikipedia.org
現代ポートフォリオ理論によると、オールカントリーの投資信託やETFが最適

以上、現代ポートフォリオ理論によると、ACWI(オール・カントリー・ワールド・インデックス)のような全世界の株式を時価総額加重平均型に保有した投資信託やETFがリスクに対してのリターンが最大化され、理論上最も合理的であると言えます。
おすすめの投資信託やETFについて詳しく知りたい方は下記の記事をご覧くださいませ。
最後に
以上、現代ポートフォリオ理論について解説してきました。上記の情報は基本、英語でしか載っていなく筆者も最初は英語で勉強したのちに、本記事で和訳して解説してきました。
金融に関する情報は日本語だけで得ようとするとかなり限られてしまう中、下記の記事でご紹介しているように、日本語だけでも金融を深く勉強できる書籍などもわずかにございます。
本記事が投資を勉強する上で、参考になりましたら望外の喜びでございます。Twitterやネットでの拡散も大歓迎ですので何卒宜しくお願い致します。
引き続き何卒宜しくお願い致します。
